What is the Child Thinking?
The very last bit of Chapter 3 – The Principles of Teaching in Kamii’s book Number in Preschool and Kindergarten explores the teacher’s role as an investigator into the child’s mind to determine what the child was thinking when he performed a mathematical operation.
Figure out how the child is thinking, and intervene according to what seems to be going on in his head.
Rather than focusing on the “error” the teacher should focus on the thinking patterns of the child that led him to the error. Kamii writes, “Just as there are many ways of getting the wrong answer, there are many ways of getting the right answer” (p. 42). That means that in order to support the child’s emerging logico-mathematical understandings we need to uncover what the s current understandings are that led them to the wrong conclusion. Correcting the error does not help the child construct knowledge. Focusing on the thinking and providing alternate ways of approaching the problem will lead to new constructions.
This past week I was observing a group of children halving and doubling numbers. The teachers provided each child with a small dry-erase board and markers so they could illustrate the problem. (This activity was done after a week of using manipulatives to halve and double numbers).
The teacher described the problem like this:
There is a boy (Frank) and a girl (Alice) and they each have an envelope. The teacher has 10 pictures and wants to divide the pictures evenly between the two children. How can we figure out how many pictures each child gets?
The teacher taped 2 large envelopes on the wall and showed the children the 10 pictures. Each of these was taped to the wall as well. The children then tried to figure out a sensible way to divide the pictures.
One child simply wrote the number 10 on his board with some other depictions of the envelopes and then he stopped. He wasn’t sure how to proceed. The teacher approached the child with smaller versions of the envelopes and pictures and used them as manipulatives so he could physically divide them. In this example, the teacher considered the child’s thinking based on her observations of his attempts and provided additional support as needed.
The above drawing is called “the intuitive approach.” The child thinks globally about the problem and eyeballs it to get the answer. He may be right, which is a function of “chance,” but he may also be wrong as he is probably just as likely to eyeball it incorrectly as correctly. Guessing in this way reveals that the child does not have the logico-mathematical skills to approach this problem using number sense, number rules, or one-to-one correspondence. It is the teacher’s job to determine that the child’s thinking is not yet ready for this difficult problem and then to provide more appropriate questions for him.
In “a spatial approach” the child lines the pictures up in a one-to-one correspondence pattern in order to create 2 sets of pictures. If these line up equally, the sets can be distributed to Alice and Frank evenly. Once divided, the child can count the sets to determine “how many” each Frank and Alice received. In the picture below, the child lined up the numbers 1-5 and the numbers 7-10 (you can see that he missed the number ‘6’). I am not sure but I think that this child counted each numeral and came up with ‘5’ for each set because he counted the ‘1’ and the ‘0’ as separate numerals although together, they represent one number – ’10’.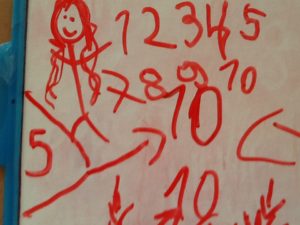
In the picture below, the child drew her own envelopes and then drew a square in each envelope (representing the pictures). She continued doing this until she had drawn 10 squares and the 10 pictures were divided equally. This is called “the logical approach.” The child’s logic is well-developed as he has developed a “procedure” that will always work to solve this sort of problem.
Through observation, the teacher can determine which approach each child is using to solve the problem and then influence the child’s thinking process rather than giving the answer or solving the problem for the child.
